Quizz Enigmes...
"Réfléchir? :o"
| Page : 1 2 3 4 5 6 7 | ||
| Pseudo | Messages | |
|---|---|---|
| Page : 1 2 3 4 5 6 7 | ||
|
Fenrill -
Publié le 15/06/2013 à 12:02:43 |
||
|
Je suis assez fan d'énigmes en tout genre, c'est pourquoi j'ouvre ce topic. Histoire de se poser des énigmes à tour de rôle et se creuser la cervelle (ou tricher sur internet, c'est à voir). Je commence : Un homme se nomme Jean-Pierre. Jean-Pierre, nostalgique, marche sur la plage. Et quand il se retourne, il ne voit pas ses traces de pas. Pourquoi donc? |
||
|
Roi of the Suisse -
Publié le 15/06/2013 à 13:39:02 |
||
 Membre 298 messages |
Parce qu'il marchait à reculons, donc ses pas étaient devant lui ! | |
|
Fenrill -
Publié le 15/06/2013 à 13:40:48 |
||
|
Bien joué, à toi ^-^ (énigme préférée des loup-garousques!  )
|
||
|
Roi of the Suisse -
Publié le 15/06/2013 à 15:57:45 |
||
|
Membre 298 messages |
Alors voici la carte d'une planète :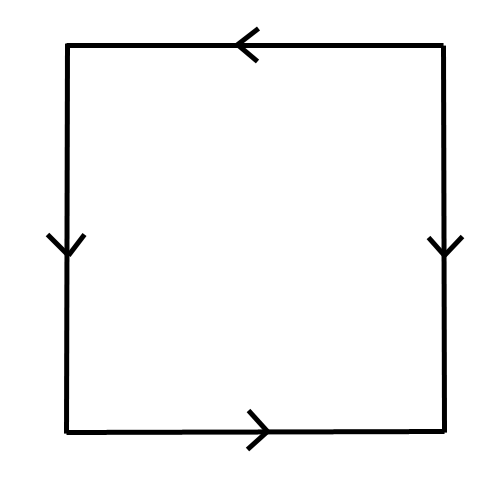 La carte "boucle". Les côtés gauche et droit se touchent, les côtés haut et bas se touchent. Cependant, les côtés gauche et droit se touchent dans le même sens, alors que les côtés haut et bas se touchent dans le sens contraire (par exemple si sur le côté haut un point est près du bord gauche, en bas il sera prêt du bord droit. 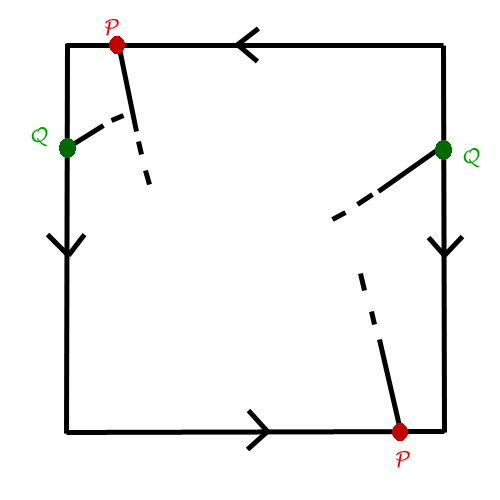 Sur cette planète il y a plein de pays délimités par des frontières, la frontière se prolonge d'un côté à l'autre du carré (en symétrie axiale verticale pour les côtés verticaux, en symétrie centrale pour les côtés horizontaux, comme expliqué précédemment). Pour que la carte soit jolie, on colorie les pays qui se touchent avec des couleurs différentes : 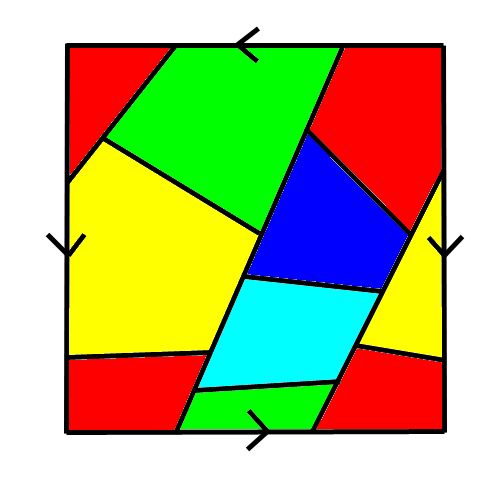 (ici chacun des 5 pays touche les 4 autres, donc il faut 5 couleurs minimum) 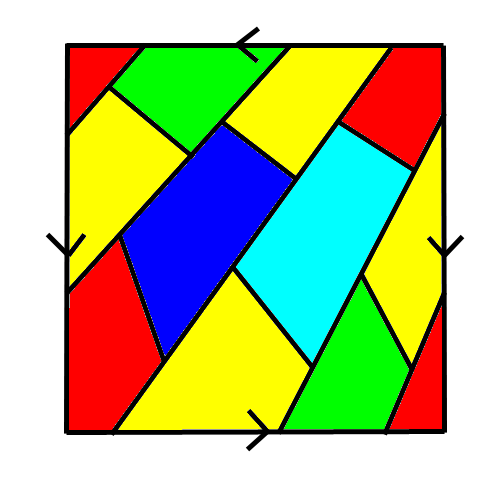 (ici les deux pays jaunes ne se touchent pas : on peut utiliser la même couleur) (on remarque d'ailleurs l'inversion de l'ordre des couleurs entre le côté haut et le côté bas du carré) Voici la même carte coloriée avec plus de couleurs qu'il n'en suffisait : 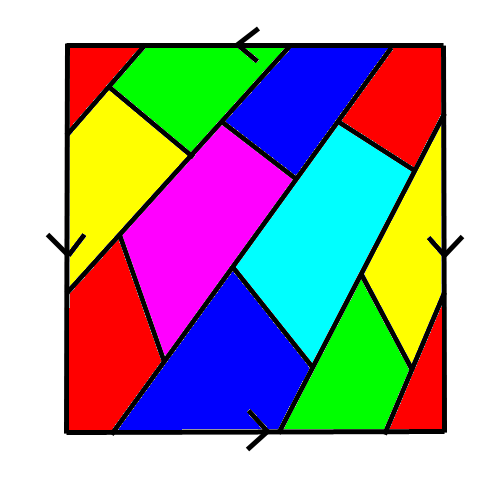 Cette solution n'est pas optimisée. Donc il faut bien vérifier en ajoutant une nouvelle couleur qu'on ne pouvait pas faire autrement ! Quel est le plus petit nombre de couleurs qui permet de colorier TOUTES les cartes possibles sur cette planète ? Donner une carte qui illustre ce cas extrême. De préférence une carte la simple possible : avec autant de pays que de couleurs. 
Edité pour la dernière fois le 15/06/2013 à 21:37:19.
|
|
|
garsim -
Publié le 16/06/2013 à 21:59:08 |
||
 Ce sont les choses qu'on aime qui font ce qu'on est. Membre 1174 messages |
A tout hasard... Edit : whoops j'avais oublié le fait que les pays se touchent sur les bords.  Forget it.Puis en plus, je ne suis même pas sûr d'avoir compris l'énoncé en fait. 
Edité pour la dernière fois le 16/06/2013 à 22:05:36.
|
|
|
Roi of the Suisse -
Publié le 16/06/2013 à 22:25:51 |
||
|
Membre 298 messages |
Ca peut pas être trois vu que j'ai moi-même présenté une carte qui nécessitait 5 couleurs. Le nombre de couleurs doit servir à colorier toutes les cartes qu'il est possible d'imaginer dans ce carré. |
|
|
garsim -
Publié le 16/06/2013 à 22:40:50 |
||
|
Ce sont les choses qu'on aime qui font ce qu'on est. Membre 1174 messages |
Mmh... il y a quelque chose que je ne comprends pas trop quand même. Si j'ai bien compris la logique de la "boucle", si j'essaie de la schématiser en copiant/collant la carte de sorte à la "prolonger" naturellement, comme je le ferais avec un planisphère, sur ton dernier exemple ça donnerait ça : Sauf qu'il y a des zones qui communiquent, d'un seul coup, alors qu'elles ne devrait pas... (et même si mon copier/coller n'est pas fait au détail, quand même, il y a bien un petit problème de raccordement) |
|
|
Roi of the Suisse -
Publié le 17/06/2013 à 01:35:17 |
||
|
Membre 298 messages |
Nan mais mon schéma est fait à l'arrache hein  Et arrête de reprendre toujours ma carte ! Invente-t-en une toi-même rien qu'à toi !  La mienne n'a besoin que de 5 couleurs de toutes façons, c'est pas assez. |
|
|
Roi of the Suisse -
Publié le 20/06/2013 à 15:06:59 |
||
|
Membre 298 messages |
Bon, laissez tomber, la réponse était 6, et voici la carte :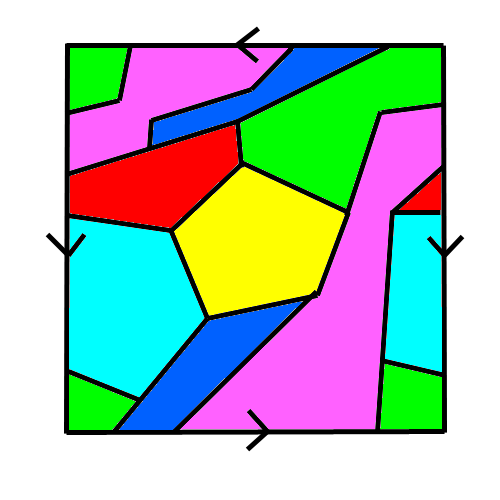
|
|
|
Roi of the Suisse -
Publié le 20/06/2013 à 15:08:18 |
||
|
Membre 298 messages |
Autre énigme : Comment découper un carré en 7 triangles de même aire ?
Edité pour la dernière fois le 20/06/2013 à 15:08:32.
|
|
|
garsim -
Publié le 20/06/2013 à 19:01:22 |
||
|
Ce sont les choses qu'on aime qui font ce qu'on est. Membre 1174 messages |
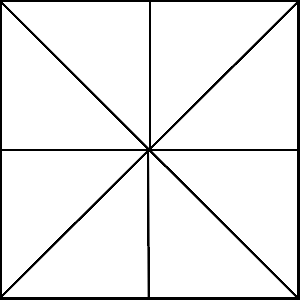 T'as pas précisé qu'il en fallait exactement sept. Là, il y en a au moins sept, donc a priori, ça passe.  (si ça se trouve, c'est peut-être ça l'astuce, qui ne tente rien n'a rien...) Au passage... il y avait une stratégie particulière pour résoudre ton énigme précédente ? |
|
|
Raistlin -
Publié le 20/06/2013 à 19:40:59 |
||
 Bon, là c'est mal fait, hein, mais dans l'idée, c'est ça, non ? (avec le triangle en haut à gauche possédant ses côtés égaux à racine de 2 sur 7). L'agonie, c'est l'art de rester sur sa fin.
|
||
|
AlexRE -
Publié le 20/06/2013 à 20:35:17 |
||
 Amateur, Blablateur, Webmaster 4362 messages |
Oui mais pas de même aire ! Pas bête Raistlin ! http://www.alexzone.net/
shûji : "un alex roi c'est le O+ du groupe sanguin, il aime tout, les awards il a pas de préférence, il fait des tests élaboré, note normal, il est casable partout ~ juste qu'il faut prévoir 2 semaines d'avance avec lui pouce vert etc" |
|
|
garsim -
Publié le 20/06/2013 à 22:16:37 |
||
|
Ce sont les choses qu'on aime qui font ce qu'on est. Membre 1174 messages |
Comment ça pas de même aire ?  Ca se voit qu'ils ont isométriques (donc ils ont forcément la même aire) pourtant non ? Mais la solution de Raistlin doit être la bonne (fallait y penser !) |
|
|
Roi of the Suisse -
Publié le 21/06/2013 à 12:59:13 |
||
|
Membre 298 messages |
Nan. Caca boudin. Oui, essayer de faire que chacune des 6 zones touche les 5 autres, en utilisant le fait que ça ne boucle pas dans le même sens en bas. Raistlin : Le triangle du coin a une aire de 1/7, donc ses petits côtés font racine(2/7), les deux triangles en haut à droite ont un côté du dessus de (1 - racine(2/7))/2 et une hauteur de 1, donc une aire de (1 - racine(2/7))/4 ce qui est différent de 1/7 
Edité pour la dernière fois le 21/06/2013 à 12:59:38.
|
|
Vous souhaitez donner votre avis sur ce sujet ? Connectez-vous à votre compte, ou créez-vous un compte !