Quizz Enigmes...
"Réfléchir? :o"
| Page : 1 2 3 4 5 6 7 | ||
| Pseudo | Messages | |
|---|---|---|
| Page : 1 2 3 4 5 6 7 | ||
|
Roi of the Suisse -
Publié le 09/09/2013 à 15:18:45 |
||
|
Alors voici une énigme qui demande pas mal d'explications au début, mais la question à la fin est simple. Ci-dessous, un noeud : 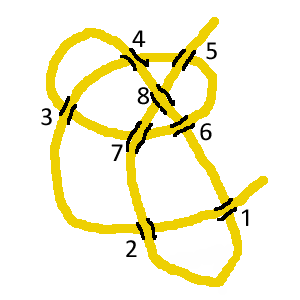 C'est une corde qui s'entrelace avec elle-même, je suppose que vous avez l'habitude de voir ce genre de choses dans vos câbles d'écouteurs. Si on tire chacune des extrémités de la corde, un noeud se forme. C'est la galère pour le défaire. Ci-dessous, un non-noeud : 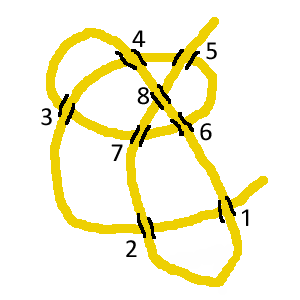 Il ressemble au précédent, mais si on regarde attentivement, on s'aperçoit qu'il ne s'agit que d'une boucle posée sur une autre boucle. Si on tire la corde aux extrémités, il n'y a pas de noeud. C'est ce que les magiciens appellent un noeud magique je suppose. Numérotons les croisements que fait la corde avec elle-même. Ici il y en a 8 à chaque fois. Partons d'une extrémité, et listons les croisements rencontrés, dans l'ordre. On précise si on passe au dessus ou bien en dessous avec un + ou un -. Pour les deux noeuds, les listes de croisements rencontrés sont : +1 -2 +3 -4 -5 +6 -7 -3 +4 +8 -6 -1 +2 +7 -8 +5 pour le vrai noeud -1 -2 +3 -4 -5 -6 -7 -3 +4 +8 +6 +1 +2 +7 -8 +5 pour le faux noeud Vérifiez que je ne me suis pas trompé (et que vous avez compris la notation) en suivant la corde avec le doigt. Maintenant, sur le bord d'un cercle, mettons dans l'ordre tous les croisements rencontrés ; puis relions les croisements de même numéro (qui sont le même croisement, une fois passé par au dessus, une fois passé par en dessous) : 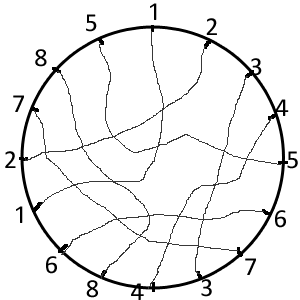 Pour préciser dans quel sens se fait le croisement, on met le long des lignes des petites flèches allant du passage sous le croisement au passage sur le croisement :  pour le vrai noeud (+1 -2 +3 -4 -5 +6 -7 -3 +4 +8 -6 -1 +2 +7 -8 +5) 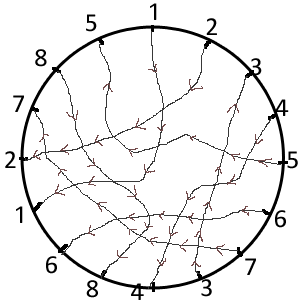 pour le faux noeud (-1 -2 +3 -4 -5 -6 -7 -3 +4 +8 +6 +1 +2 +7 -8 +5) Les flèches vont du - vers le +. Maintenant, on va tracer une "constellation" pour chacun de ces filets... Chaque maille du filet possède des flèches sur son pourtour. Interessons nous aux coins des mailles et au comportement des flèches dans ces coins : - parfois, un coin de la maille se fait pointer par deux flèches (----->-----coin-----<-----) - parfois un coin de la maille se fait fuir par les deux flèches (-----<----coin----->-----) C'est à ces deux types de coins qu'on va s'intéresser : les coins attirants et les coins repoussants. Le troisième type de coin, où les flèches ne font que passer, ne nous intéresse pas (---->----coin---->----). Quand deux lignes se croisent et forment un coin attirant, il y a un coin repoussant de l'autre côté du point de croisement. Un croisement de lignes qui comporte un coin attirant et un coin repoussant constitue une "porte" d'une maille à une autre. On marque les deux mailles par un gros point rouge, et on relie les deux points rouges par un trait qui traverse la porte, c'est-à-dire le coin repoussant et le coin attirant. 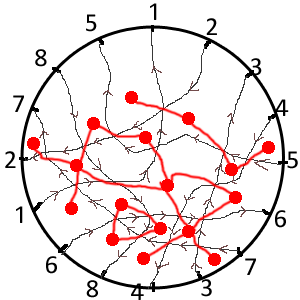 pour le vrai noeud 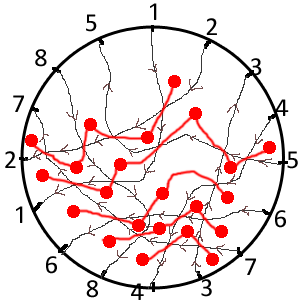 pour le faux noeud Comprenez bien comment j'ai construit ces constellations en fonction de la nature des coins des mailles des filets. Maintenant une observation de ces constellations : - Le vrai noeud a une constellation qui comporte des cycles (la ligne rouge forme des carrés, des triangles...) et des carrefours (sur certains points rouges, il y a plus de deux chemins rouges qui partent). - Le faux noeud a une constellation qui ne comporte que des lignes ! Pas de cycles, pas de carrefours. Coïncidence ? Question de l'énigme : Trouvez un vrai noeud dont la constellation ne comporte ni cycle ni carrefour, ou bien un faux noeud dont la constellation comporte un cycle ou un carrefour. |
||
|
cheikh35 -
Publié le 09/09/2013 à 22:55:34 |
||
 I'm not a hero, I'm just a Membre 494 messages |
Il y a un lien entre la numérotation des croisements et l'agencement des coins de mailles attirants/repoussants. Je vais essayer faire une petite étude avec plusieurs essais pour comprendre comment ça marche. J'imagine qu'il y a un nombre limité de solutions au problème. Donc si par un raisonnement inductif on arrive à généraliser le lien entre la nulérotation et la constellation, on pourrait déterminer toute la liste, assez fastidieuse j'imagine, des solutions au problème. Si le nombre est illimité (ce qui est peu problème compte tenu du problème), je ne proposerai qu'une solution. (genre le mec qui maîtrise le sujet  )Par contre faut que je trouve le temps de la faire  Néanmoins c'est une énigme assez intéressante ! Merci RotS Edité pour la dernière fois le 09/09/2013 à 22:56:56.
"I'm not a hero, I'm just cheikh35 ..."
|
|
|
Raistlin -
Publié le 10/09/2013 à 08:57:44 |
||
|
Ha ha ha, on dirait une b... enfin vous voyez. (Oui, je n'ai aucune capacité à représenter les choses en 3d, alors les entrelacements dessus/dessous de cordes, c'est sans moi) L'agonie, c'est l'art de rester sur sa fin.
|
||
|
Roi of the Suisse -
Publié le 11/09/2013 à 00:00:02 |
||
 Membre 298 messages |
Bon, bah je garde mes énigmes en 4D pour plus tard alors... | |
|
Kisthune -
Publié le 11/09/2013 à 09:42:27 |
||
 Membre 43 messages |
À tester avec le nœud du pendu, ça ferait ptet un truc sympa. J'ai lu ta correction sur l'autre forum, t'as pas une explication plus logique ? |
|
|
Roi of the Suisse -
Publié le 11/09/2013 à 11:26:19 |
||
|
Membre 298 messages |
Tu veux des détails ? J'ai montré l'image de la constellation, et la preuve que le noeud était faux. Tu veux quoi de plus ? Mon tour de poitrine ? 
|
|
|
Roi of the Suisse -
Publié le 11/09/2013 à 12:22:27 |
||
|
Membre 298 messages |
Ce que tu appelles noeud du pendu, c'est +1 +2 -3 -4 +5 +6 -2 -7 +8 +3 -6 -9 -10 -5 +4 +11 -12 -1 +9 +10 -11 -8 +7 +12 ? A priori il y aura pas mal de lignes, mais un ou deux cycles devraient apparaître au centre... EDIT : pour prouver que c'est bien un noeud magique, il suffit d'appliquer trois fois le théorème des dominos en repérant les 3 cycles de croisements jumeaux qui composent ce noeud. Edité pour la dernière fois le 11/09/2013 à 12:25:09.
|
|
|
Kisthune -
Publié le 11/09/2013 à 13:34:02 |
||
|
Membre 43 messages |
Le noeud du pendu est un noeud magique (c'est un peu le but d'ailleurs). Pour l'explication je parlais plutôt d'expliquer pourquoi ce n'est pas une coïncidence plutôt que montrer un contre-exemple. |
|
|
Roi of the Suisse -
Publié le 11/09/2013 à 22:03:20 |
||
|
Membre 298 messages |
Tu veux que je démontre un "théorème" dont je viens d'exhiber un contre-exemple ??? Ca va être difficile
|
|
|
cheikh35 -
Publié le 11/09/2013 à 23:15:59 |
||
|
I'm not a hero, I'm just a Membre 494 messages |
C'est l'exception qui confrime la règle ... qu'est-ce que je déteste cette phrase 
"I'm not a hero, I'm just cheikh35 ..."
|
|
|
Kisthune -
Publié le 11/09/2013 à 23:31:31 |
||
|
Membre 43 messages |
Non me suis mal exprimée. Le théorème à démontrer ce serait que peu importe le type de nœud, on peut avoir des cycles/croisements comme on peut ne pas en avoir. contre exemple c'était par rapport à la phrase "c'est une coïncidence ?" me doutais que ça induirait en erreur mais j'ai eu la flemme de changer :/ |
|
|
Roi of the Suisse -
Publié le 12/09/2013 à 13:32:09 |
||
|
Membre 298 messages |
Ben un exemple de chaque suffit dans ce cas 
|
|
|
Roi of the Suisse -
Publié le 12/09/2013 à 13:37:27 |
||
|
Membre 298 messages |
Mais à deux centimètres de ton doigt accusateur posé sur le plan, se trouve cependant un point intéressant : la conjecture que l'énigme demande d'infirmer n'est qu'à moitié fausse ! Les noeuds dont la constellation est linéaire (sans croisements ni carrefours) sont magiques. Malheurement, certains noeuds magiques tordus (le noeud du pendu, le noeud de Twistlewaite, mon noeud exemple utilisant le troisième mouvement de Reidemaster...) n'ont pas une constellation linéaire. Quand on cherche à prouver qu'un noeud est magique, on utilise la constellation qui traite pas mal de cas, mais si le test à la constellation est négatif, il faut utiliser des outils plus puissants de la théorie des noeuds, comme mes calculs noeudistiques utilisant la loi des dominos ou les transcription formelles des mouvements de Reidemaster. |
|
|
Roi of the Suisse -
Publié le 12/09/2013 à 13:38:29 |
||
|
Membre 298 messages |
+s* | |
|
cheikh35 -
Publié le 12/09/2013 à 14:50:51 |
||
|
I'm not a hero, I'm just a Membre 494 messages |
C'est intéressant. On a donc : "si un noeud a sa constellation linéaire, il est magique, réciproque étant fausse". Mais, car j'ai la flemme de faire des recherches, pourrait-tu nous en dire plus sur la loi des dominos et la théorie des noeuds (si on part pas trop en H.S.) Sinon je pense avoir trouvé un noeud solution. Je vérifié que la constellation est bien linéaire. "I'm not a hero, I'm just cheikh35 ..."
|
|
|
Kisthune -
Publié le 12/09/2013 à 16:13:21 |
||
|
Membre 43 messages |
=> J'en conclue que tu nous as induits en erreur sur l'autre forum : Tu es machiavélique ! Merci pour avoir compris ce que je n'ai pas réussi à demander clairement en 2 posts. |
|
Vous souhaitez donner votre avis sur ce sujet ? Connectez-vous à votre compte, ou créez-vous un compte !